This program simulates Buffon's Needle, a real-world experiment for estimating π's value. It's done by taking a large number of needles and dumping them on a wooden floor made of boards as wide as the needles are long. Assuming the needles land in random positions, the fraction of them that end up touching a crack between boards will be about 2/π.
What does this crude physical process have to do with π's value? It acts out a form of Monte Carlo integration. Whether a given needle hits a crack is a matter of trigonometry, so π shows up as one of the integration limits.
Monte Carlo integration is a way to estimate the area under a curve y=f(x). Take a random x between some known x0 and x1, and a random y between y0 and y1. Then find f(x): if y is less than it, the point (x, y) is under the curve (a "hit"). Note the range of x and y! All possible points (x, y) fall in a (x1 - x0) by (y1 - y0) rectangle. The fraction of this rectangle taken up by the area A under the curve is
which is also the probability of a hit. Test enough random (x, y)'s to find that probability and you can get A, the value of ∫f(x). (The integration limits, of course, are x0 and x1).
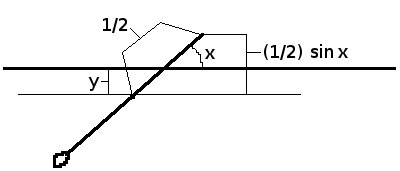
Every needle that falls will generate 2 random numbers on landing. y is the distance between the needle's midpoint and the nearest crack (in needle-lengths or floorboard-widths, to keep the math simple). x is the angle the needle makes with that crack:

The needle touches the crack if
which is exactly the condition for a hit in a Monte Carlo integration where f(x) = ½ sin x. x can be anywhere between 0 and π. (Allowing negative values of x would be redundant--the only difference between, say, π/2 and -π/2 is which end of the needle hits.) So x0 = 0, x1 = π and:
Meanwhile, since no point on a floorboard is more than half a width from the edge, y must be between y0 = 0 and y1 = ½. This is enough to show that the probability of a hit is indeed
This is actually the main purpose of the program. It's meant to test one way that Buffon's Needle might be adapted for computer simulation: the program starts with a guess at π's value and tries to refine it through successive runs of the experiment.
Buffon's Needle does not translate well to a computer model. In the real world, the laws of physics distribute x's values evenly across the interval [0, π) without any help from the experimenter. Simulating this would mean having a random number generator pick numbers in that interval, but to do that it would have to know π already. This defeats the purpose of modeling--deriving a result that wasn't given in the original data--even if it does make some spiffy demos possible.
What if the random number generator were given a wrong value of π for x's upper bound? Would the estimate derived from the simulation be any closer to the right one? If so, a true computer model of Buffon's Needle is possible--we simply have the program to do another run, feeding the new estimate of π into the generator and getting a still better estimate out. After enough runs the results should converge on π. (Well, not exactly...we're dealing with a random process that only produces rational numbers...but close enough.)
There's just one complication: the program only works if a single iteration actually does give a better value of π (on average) than it started with. As far as I know, this has never been proven. It's certainly fair to expect that this program can improve on an initial guess that's sufficiently wrong: sin x oscillates, so the monstrous x's that result from a guess of π = 10,000 will behave just like x's between 0 and the real π (though they won't be quite so evenly distributed). Other than that, I have no idea what (if anything) about the mathematics of the problem would make this program work.
But work it certainly seems to. With default settings, it manages to begin generating values around π in less than a dozen trials regardless of whether the initial guess is something reasonable like 3 or absurd like 0.001. The only guess that seems to break the simulation is 0. How close it gets to π is limited by the element of chance in individual trials, but the average for all iterations tends to be correct to 2 decimal places.
I have not experimented much with varying the number of iterations or the number of needles thrown per iteration. Reducing these would probably hurt the accuracy, but I don't know by how much. Feel free to try it.